尽管网络上讲述 线性回归 的文章多如牛毛，这里再次讲述，仅为记录自己的理解过程。

机器学习过程

一个典型的有监督的机器学习过程，目标是构建一个具有较强泛化能力的模型，这个模型能够对输入数据得到输出数据，输出数据能够进行较好的预测。

在构建模型的过程中，首先给出一组已经标注好的训练数据作为输入，通过定义一个假设函数对输入数据进行拟合，并通过定义一个损失函数衡量假设函数拟合的好坏，在损失函数取得最小值时，确定假设函数中参数。这个假设函数就作为要构建的模型，对新的数据给出估计。

线性回归

训练数据集 $\{(X^{(1)},y^{(2)}),(X^{(2)},y^{(2)}),\cdots,(X^{(m)},y^{(m)})\}$，其中，$X^{(i)}, (1 \leq i \leq m)$ ，为一组向量 $(x_{1}^{(i)}, x_{2}^{(i)}, \cdots, x_{n}^{(i)})$，分量 $x_{j}^{(i)}, (1 \leq j \leq n)$， 为 $X^{(i)}$ 的一个特征，$y^{(i)} \in R$。

假设函数

线性回归假设 $X^{(i)}$ 的特征 $x_{j}^{(i)}, (1 \leq j \leq n)$ ，和结果 $y^{(i)}$ 满足线性关系。这里，我们定义假设函数

$$h_{\theta}(X)=\theta_{0}+\theta_{1}x_{1}+\theta_{2}x_{2}+\cdots+\theta_{n}x_{n}$$

$\theta$ 在这里为需要估计参数，即每个特征的的影响力。如果令 $x_{0}=1$，则假设函数为

$$h_{\theta}(X)=\theta^{T}X.$$

损失函数

$\theta$ 的取值有无限多个，如何评估哪个取值较好，需要对定义的假设函数 $h_{\theta}(X)$ 进行评估。显然，关键在于衡量 $h_{\theta}(X)$ 和 $y$ 之间的差别。

均方误差是回归任务中最常用的性能度量，因此，这里我们试图让均方误差最小化。均方误差有非常好的几何意义，它对应了常用的欧几里得距离或简称“欧氏距离(Euclidean distance)”。基于均方误差最小化来进行模型求解的方法称为 “最小二乘法(least square method)”。在线性回归中，最小二乘法就是试图找到一条直线，使得所有样本到直线上的欧氏距离之和最小。

这里，均方误差作为损失函数(Loss Function)，衡量 $h_{\theta}(X)$ 和 $y$ 之间的差别，描述 $h_{\theta}(X)$ 函数的不好程度。下面，我们称损失函数为 $J(\theta)$。

$$J(\theta)=\frac{1}{2}\sum_{i=1}^{m}(h_{\theta}(X^{(i)})-y^{(i)})^{2}$$

前面乘上 $\frac{1}{2}$ 是为了在求导的时候，这个系数就消掉了。

我们要选择最优的 $\theta$，使得 $h_{\theta}(X)$ 逼近真实值。这个问题就转化为求解最优的 $\theta$，使损失函数 $J(\theta)$ 取最小值。

$$\min_{\theta}J(\theta)$$

最小均方算法

最小均方算法(Least mean square，LMS算法)的思路是：首先给 $\theta$ 一个初始值，然后改变 $\theta$ 的值让 $J(\theta)$ 的取值不断变小，不断重复改变 $\theta$ 使 $J(\theta)$ 变小的过程直至 $J(\theta)$ 约等于最小值。

先来看当训练样本只有一个的时候的情况，然后再将训练样本扩大到多个的情况。

对 $J(\theta)$ 中每个 $\theta_{j}$ 求偏导，给 $\theta_{j}$ 一个初试值，然后向着让 $J(\theta)$ 变化最大的方向更新 $\theta_{j}$ 的取值，如此迭代

$$\theta_{j+1}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}}J(\theta)$$

公式中 $\alpha$ 称为步长（learning rate），它控制 $\theta$ 每次向 $J(\theta)$ 变小的方向和迭代时的变化幅度。$J(\theta)$ 对 $\theta$ 的偏导表示 $J(\theta)$ 变化最大的方向。由于是求极小值，因此梯度方向是偏导的反方向。求解过程如下：

$$
\begin{eqnarray}
\frac{\partial}{\partial \theta_{j}}J(\theta) & = & \frac{\partial}{\partial \theta_{j}}\frac{1}{2}(h_{\theta}(X)-y)^{2} \\
{} & = & 2 \cdot \frac{1}{2}(h_{\theta}(X)-y)\cdot \frac{\partial}{\partial \theta_{j}}(h_{\theta}(X)-y) \\
{} & = & (h_{\theta}(X)-y)\cdot \frac{\partial}{\partial \theta_{j}}(\sum_{i=0}^{n}\theta_{i}x_{i}-y) \\
{} & = & (h_{\theta}(X)-y)x_{j}
\end{eqnarray}
$$

$\theta$ 的迭代公式就变为：

$$\theta_{j+1}:=\theta_{j}+\alpha (y^{(i)}-h_{\theta}(X^{(i)}))x_{j}^{(i)}$$

这是当训练集只有一个样本时的数学表达。可以通过 梯度下降（gradient descent） 和 正则方程（The normal equations） 将只有一个样本的数学表达转化为样本为多个的情况。

梯度下降

批梯度下降（batch gradient descent）

批梯度下降每一步都是计算的全部训练集的数据。

$
\textrm{Repeat until convergence \{}\\
\begin{equation}
\qquad \qquad \theta_{j+1}:=\theta_{j}+\alpha \sum_{i=1}^{m} (y^{(i)}-h_{\theta}(X^{(i)}))x_{j}^{(i)}, \textrm{(for each j)}
\end{equation}\\
\textrm{\}}
$

梯度下降可能得到局部最优，但在优化问题里已经证明线性回归只有一个最优点，因为损失函数 $J(\theta)$ 是一个二次的凸函数，不会产生局部最优的情况（假设学习步长α不是特别大）。

批梯度下降的算法执行过程如下图

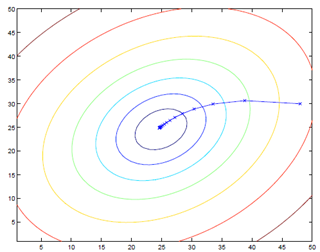
批量梯度下降每次迭代的时候都要对所有数据集样本计算求和，计算量就会很大，尤其是训练数据集特别大的情况。

随机梯度下降（Stochastic Gradient Descent, SGD）

随机梯度下降在计算下降最快的方向时，随机选一个数据进行计算，而不是扫描全部训练数据集，这样就加快了迭代速度。随机梯度下降并不是沿着 $J(\theta)$ 下降最快的方向收敛，而是以震荡的方式趋向极小点。

随机梯度下降迭代公式如下

$
\textrm{Loop \{}\\
\qquad \textrm{for i=1 to m \{}\\
\begin{equation}
\qquad \qquad \theta^{‘}_{j}:=\theta_{j}+\alpha (y^{(i)}-h_{\theta}(X^{(i)}))x_{j}^{(i)}, \textrm{(for each j)}
\end{equation}\\
\qquad \textrm{\}}\\
\textrm{\}}
$

执行过程如下图

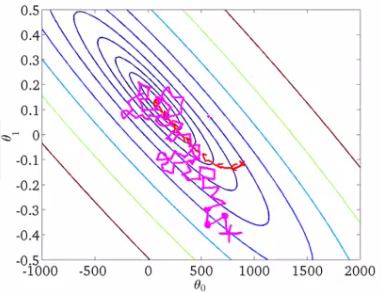
总结

线性回归是回归问题中的一种，假设特征值与目标值之间满足线性相关，即满足一个多元一次方程。通过使用最小二乘法构建损失函数，用梯度下降求解损失函数最小时的参数 $\theta$。

参考资料

1. 对线性回归，logistic回归和一般回归的认识
2. 机器学习算法比较
3. 线性回归、梯度下降（Linear Regression、Gradient Descent）
4. 周志华，《机器学习》，清华大学出版社