Google的《机器学习速成课程》学习笔记一
Google的《机器学习速成课程 》主要从 机器学习概念、机器学习工程 和 机器学习现实世界应用示例 三方面介绍了机器学习。我学完后对速成课程的感受是,对机器学习中的概念解释非常透彻,对机器学习中的部分算法通过动画的方式演示非常直观,概念解释结合示例说明非常丰富,推荐给要学习机器学习的伙伴!
就我在学习课程过程中记录的知识点进行整理,以便之后再温故~
问题的构建:机器学习主要术语
什么是(监督式)机器学习?简单来说,它的定义为:机器学习系统通过学习如何组合输入信息来对从未见过的数据做出有用的预测。
标签
我们要预测的事物,即简单线性回归中的 $y$ 变量。标签可以是小麦未来的价格、图片中显示的动物品种、音频剪辑的含义或任何事物。
特征
输入变量,即简单线性回归中的 $x$ 变量。简单的机器学习项目可能会使用单个特征,而比较复杂的机器学习项目可能会使用数百万个特征,按如下方式指定 $\{x_{1}, x_{2}, \cdots, x_{N}\}$。在垃圾邮件中,特征可能包括 电子邮件文本中的字词、发件人的地址、发送电子邮件的时段。
样本
数据的特定实例:$X$。(我们采用粗体 $X$ 表示它是一个矢量。)我们将样本分为以下两类:有标签样本,无标签样本。有标签样本同时包含特征和标签,即
1 | labeled examples: {features, label}: (x, y) |
我们使用有标签样本来训练模型。在我们的垃圾邮件检测器示例中,有标签样本是用户明确标记为“垃圾邮件”或“非垃圾邮件”的各个电子邮件。
无标签样本包含特征,但不包含标签。即:
1 | unlabeled examples: {features, ?}: (x, ?) |
在使用有标签样本训练了我们的模型之后,我们会使用该模型来预测无标签样本的标签。在垃圾邮件检测器示例中,无标签样本是用户尚未添加标签的新电子邮件。
模型
定义了特征与标签之间的关系。例如,垃圾邮件检测模型可能会将某些特征与“垃圾邮件”紧密联系起来。
模型生命周期的两个阶段:
- 训练 表示创建或学习模型。也就是说,您向模型展示有标签样本,让模型逐渐学习特征与标签之间的关系。
- 推断 表示将训练后的模型应用于无标签样本。也就是说,您使用训练后的模型来做出有用的预测 ($y^{‘}$)。例如,在推断期间,您可以针对新的无标签样本预测。
回归与分类
回归 模型可预测连续值。例如,回归模型做出的预测可回答如下问题:
- 加利福尼亚州一栋房产的价值是多少?
- 用户点击此广告的概率是多少?
分类模型可预测离散值。例如,分类模型做出的预测可回答如下问题:
- 某个指定电子邮件是垃圾邮件还是非垃圾邮件?
- 这是一张狗、猫还是仓鼠图片
训练与损失
训练模型表示通过有标签样本来学习(确定)所有权重和偏差的理想值。在监督式学习中,机器学习算法通过以下方式构建模型:检查多个样本并尝试找出可最大限度地减少损失的模型;这一过程称为经验风险最小化。
损失是对糟糕预测的惩罚。也就是说,损失 是一个数值,表示对于单个样本而言模型预测的准确程度。如果模型的预测完全准确,则损失为零,否则损失会较大。训练模型的目标是从所有样本中找到一组平均损失“较小”的权重和偏差。
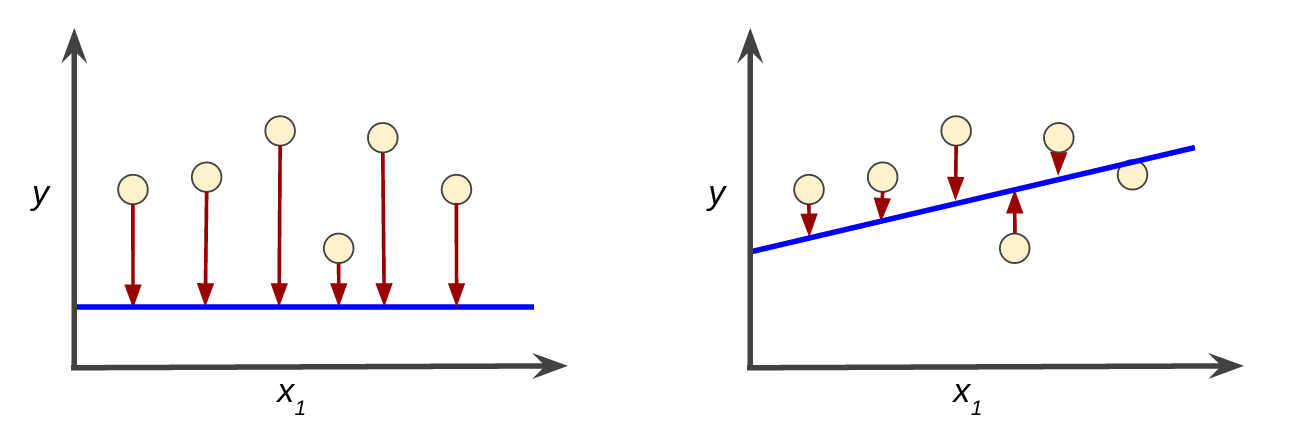
平方损失:一种常见的损失函数
接下来我们要看的线性回归模型使用的是一种称为平方损失(又称为 $L_{2}$ 损失)的损失函数。单个样本的平方损失如下:
$
= \text{the square of the difference between the label and the prediction} \\
= (observation - prediction(x))^{2} \\
= (y - y^{‘})^{2}
$
均方误差 (MSE) 指的是每个样本的平均平方损失。要计算 MSE,请求出各个样本的所有平方损失之和,然后除以样本数量:
$$MSE=\frac{1}{2}\sum_{(x,y)\in D}(y-prediction(x))^{2}$$
其中:
- $(x, y)$ 指的是样本,其中
- $x$ 指的是模型进行预测时使用的特征集(例如,温度、年龄和交配成功率)
- $y$ 指的是样本的标签(例如,每分钟的鸣叫次数)
- $prediction(x)$ 指的是权重与偏差和特征集$x$结合的函数。
- $D$ 指的是包含多个标签样本的数据集
- $N$ 指的是 $D$ 中的样本数量

