逻辑回归
逻辑回归(Logistic Regression)是机器学习中有监督学习的分类模型,应用于二分类问题,或者说用来分类0/1问题,也就是预测结果属于0或者1的二值分类问题。
在电商中,逻辑回归常用于预测一个用户是否点击特定的商品,应用于排序等场景中。
分类问题
对于某个分类任务,如判定一封邮件是否为垃圾邮件,我们需要通过分类器预测分类结果
- 是(记为1)
- 不是(记为0)
如果考虑 0 就是“不发生”,1 就是“发生”,那么可以将分类任务理解成估计事件发生的概率 $p$,通过事件发生概率的大小来达到分类目的。因此,我们需要使得预测结果即概率值限定在 $[0, 1]$ 之间。
如果仍然采用线性回归,$p=f_{\theta}(X)=\theta ^{T}X$ 作为分类器,其预测值可能会远远大于1或者远远小于0,不符合预期想法。
logistic函数
逻辑回归引入logistic函数,将分类器输出界定在 $[0, 1]$ 之间,其一般形式可表示为
$$f_{\theta}(X)=g(\theta ^{T}X)$$
问题变为选择什么形式的logistic函数。
首先,选用 优势比Odds 代替概率,优势比是事件发生概率和不发生概率之间的比值,记为
$$odds=\frac{p}{1-p}$$
通过该变换,可以将 $[0, 1]$ 之间的任意数映射到 $[0, \infty]$ 之间的任意实数,但是,线性回归的输出还可以是负数,我们还需要另一步变换将 $[0, \infty]$ 的实数域映射到实数域 $R$ 空间;
然后,在众多非线性函数中,$log$ 函数的值域为整个实数域且单调,因此,我们可以计算优势比的对数,令
$$\eta=log(odds)=log\frac{p}{1-p}=logit(p).$$
经过以上两步,我们可以去除分类问题对因变量值域的限制,如果概率等于0,那么优势比则为0,$logit$ 值为 $-\infty$;相反,如果概率等于1,优势比为 $\infty$,$logit$ 值为 $\infty$。因此,$logit$ 函数将范围为 $[0, 1]$ 的概率值映射到整个实域空间,当概率值小于 0.5 时,$logit$ 值为负数,反之,$logit$ 值为正数。
综上所述,我们解决了分类问题对分类器预测的因变量值域的限制,我们就可以采用线性回归对一一映射后的概率值进行线性拟合,即
$$logit(p)=log(\frac{p}{1-p})=\eta=f_{\theta}(X)=\theta^{T}\cdot X.$$
因为 $logit$ 变换是一一映射,所以存在 $logit$ 的反变换 $antilogit$,我们可以求得
$$p=antilogit(X)=\frac{e^{\eta}}{1+e^{\eta}}=\frac{e^{\theta^{T}\cdot X}}{1+e^{\theta^{T}\cdot X}}$$
$$1-p=1-antilogit(X)=1-\frac{e^{\eta}}{1+e^{\eta}}=1-\frac{e^{\theta^{T}\cdot X}}{1+e^{\theta^{T}\cdot X}}=\frac{1}{1+e^{\theta^{T}\cdot X}}$$
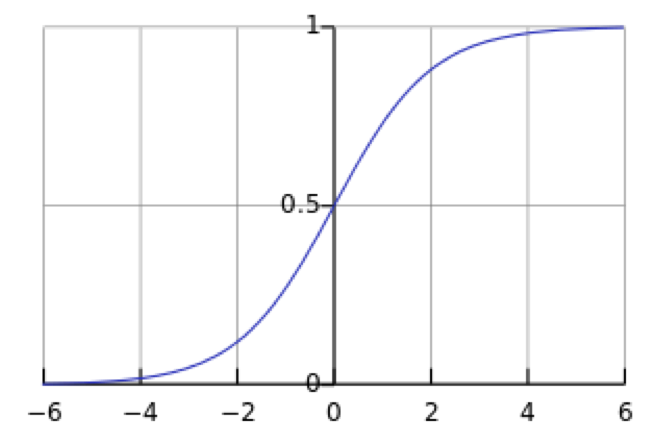
上式即为logistic回归的一般表达式,其采用的 $logit$ 变换一般记为sigmoid函数
$$g(\theta^{T}\cdot X)=\frac{e^{\theta^{T}\cdot X}}{1+e^{\theta^{T}\cdot X}}=\frac{1}{1+e^{-\theta^{T}\cdot X}}$$
sigmoid函数的曲线如下图
最大似然估计
通过上述分析,可以获得logistic回归的表达式
$$P(y=1|X)=\frac{exp(\theta^{T}\cdot X)}{1+exp(\theta^{T}\cdot X)}$$
$$P(y=0|X)=\frac{1}{1+exp(\theta^{T}\cdot X)}$$
其中,$\theta$ 是需要估计的参数。假设有一组观测样本,那么现在的任务就变成给定一组数据和一个参数待定的模型下,如何估计模型参数的问题。
最大似然估计是估计未知参数的一种方法,最大似然估计(Maximum Likelihood Method)是建立在各样本间相互独立且样本满足随机抽样(可代表总体分布)下的估计方法,它的核心思想是如果现有样本可以代表总体,那么最大似然估计就是找到一组参数使得出现现有样本的可能性最大,即从统计学角度需要使得所有观测样本的联合概率最大化,又因为样本间是相互独立的,所以所有观测样本的联合概率可以写成各样本出现概率的连乘积,即:
$$\prod_{i=1}^{m}\underbrace{ P(y^{(i)}=1|X^{(i)}) }_{ \textrm{where $1 \leq i \leq m$ and $y^{(i)}=1$} }\cdot \underbrace{ P(y^{(i)}=0|X^{(i)}) }_{ \textrm{where $1 \leq i \leq m$ and $y^{(i)}=0$} }=\prod_{i=1}^{m}P(y^{(i)}=1|X^{(i)})^{y^{(i)}}\cdot P(y^{(i)}=0|X^{(i)})^{1-y^{(i)}}$$
通过观察我们可以看出,当样本响应变量为1时,上式等于 $P(y^{(i)}=1|X^{(i)})$;当样本响应变量为0时,上式等于 $P(y^{(i)}=0|X^{(i)})$,是所有样本边际分布概率的连乘积,通常被称之为似然函数 $\ell(\theta)$。
最大似然估计的目标是求得使得似然函数 $\ell(\theta)$ 最大的参数 $\theta$ 的组合,理论上讲我们就可以采用梯度上升算法求解该目标函数(似然函数)的极大值。但是上式不是凸函数,在定义域内为非凸函数,具体形式如下
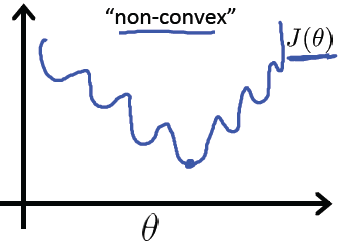
之前线性回归可以采用梯度下降算法求解是因为线性回归的损失函数(均方误差函数)是凸函数,为碗状,而凸函数具有良好的性质(对于凸函数来说局部最小值点即为全局最小值点)使得我们一般会将非凸函数转换为凸函数进行求解。因此,最大似然估计采用自然对数变换,将似然函数转换为对数似然函数,其具体形式为
$$
\begin{eqnarray}
log(\ell (\theta)) & = & log(P(y^{(i)}=1|X^{(i)})^{y^{(i)}}\cdot P(y^{(i)}=0|X^{(i)})^{1-y^{(i)}}) \\
{} & = & \sum_{i=1}^{m}(y^{(i)}log(g(\theta^{T}X^{(i)}))+(1-y^{(i)})log(1-g(\theta^{T}X^{(i)})))
\end{eqnarray}
$$
相对于求解对数似然函数的最大值,我们当然可以将该目标转换为对偶问题,即求解损失函数 $J(\theta)=-log(\ell (\theta))$ 的最小值。因此,我们定义logistic回归的损失函数为
$$J(\theta)=-log(\ell (\theta))=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}log(g(\theta^{T}X^{(i)}))+(1-y^{(i)})log(1-g(\theta^{T}X^{(i)})))$$
从损失函数的直观表达上来看,当 $y^{(i)}=1,g(\theta^{T}X^{(i)})=1$ 时(预测类别和真实类别相同),$J(\theta | X^{(i)})=0$;当 $y^{(i)}=1,g(\theta^{T}X^{(i)}) \to 0$ 时(预测类别和真实类别相反),$J(\theta | X^{(i)}) \to \infty$。这意味着,当预测结果和真实结果越接近时,预测产生的代价越小,当预测结果和真实结果完全相反时,预测会产生很大的惩罚。该理论同样适用于 $y^{(i)}=0$ 的情况。
最大似然估计求解
有了损失函数,我们自然可以选用梯度下降算法或者其他优化算法对目标函数进行求解。对于梯度下降算法,我们可以通过求解目标函数的一阶偏导数获得梯度,为
$$
\begin{eqnarray}
\frac{\partial}{\partial \theta_{j}}J(\theta) & = & -\sum_{i=1}^{m}(\frac{y^{(i)}}{g(\theta^{T}X^{(i)})}-\frac{1-y^{(i)}}{1-g(\theta^{T}X^{(i)})})\cdot g^{‘}(\theta^{T}X^{(i)}) \\
{} & = & -\sum_{i=1}^{m}((\frac{y^{(i)}}{g(\theta^{T}X^{(i)})}-\frac{1-y^{(i)}}{1-g(\theta^{T}X^{(i)})})\cdot ((1-g(\theta^{T}X^{(i)}))\cdot g(\theta^{T}X^{(i)})\cdot \frac{\partial \theta^{T}X^{(i)}}{\partial \theta_{j}})) \\
{} & = & -\sum_{i=1}^{m}(y^{(i)}(1-g(\theta^{T}X^{(i)}))-(1-y^{(i)})g(\theta^{T}X^{(i)}))\cdot X^{(i)}_{j} \\
{} & = & -\sum_{i=1}^{m}(g(\theta^{T}X^{(i)})-y^{(i)})\cdot X^{(i)}_{j}
\end{eqnarray}
$$
因此,梯度更新的表达式为
$$
\theta^{‘}_{j}:=\theta_{j}+\alpha\sum_{i=1}^{m}(g(\theta^{T}X^{(i)})-y^{(i)})\cdot X^{(i)}_{j}, \textrm{(for each j)}
$$
逻辑回归和线性回归
在谈两者关系之前,需要讨论的是,逻辑回归中使用到的sigmoid函数到底起到了什么作用。
下图的例子中,需要判断肿瘤是恶性还是良性,其中横轴是肿瘤大小,纵轴是线性函数 $h_{\theta}(X)=\theta^{T}\cdot X$ 的取值,因此在左图中可以根据训练集(图中的红叉)找到一条决策边界,并且以 0.5 作为阈值,将 $h_{\theta}(X) \geq 0.5$ 情况预测为恶性肿瘤,这种方式在这种数据比较集中的情况下好用,但是一旦出现如右图中的离群点,它会导致学习到的线性函数偏离(它产生的权重改变量会比较大),从而原先设定的0.5阈值就不好用了,此时要么调整阈值要么调整线性函数。
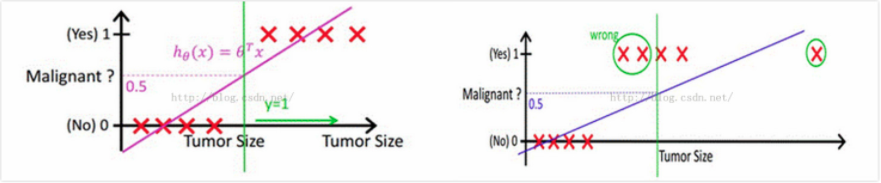
如果我们调节阈值,在这个图里线性函数取值看起来是0~1,但是在其他情况下可能就是从 $-\infty$ 和 $\infty$,所以阈值的大小很难确定,假如能够把 $\theta^{T}\cdot X$ 的值变换到一个能控制的范围那么阈值就好确定了,所以找到了sigmoid函数,将 $\theta^{T}\cdot X$ 值映射到了 $(0, 1)$,并且解释成概率。而如果调节线性函数,那么最需要的是减少离群点的影响,离群点往往会导致比较大的 $|\theta^{T}\cdot X|$ 值,通过sigmoid函数刚好能够削弱这种类型值的影响,这种值经过sigmoid之后接近0或者1。因此可以说sigmoid在逻辑回归中起到了两个作用
- 将线性函数的结果映射到了$(0, 1)$;
- 减少了离群点的影响。
逻辑回归看似就是线性回归,它们俩都要学习一个线性函数,逻辑回归无非是多加了一层函数映射,但线性回归是在拟合输入向量 $X$ 的分布,而逻辑回归中的线性函数是在拟合决策边界,它们的目标是不一样的。
线性回归和逻辑回归是属于同一种模型,但是它们要解决的问题不一样,前者解决的是regression问题,后者解决的是classification问题,前者的输出是连续值,后者的输出是离散值,而且前者的损失函数是输出 $y$ 的高斯分布,后者损失函数是输出的伯努利分布。
总结
本文先从判定一封邮件是否为垃圾邮件的分类问题开始,预测分类结果,并通过事件发生概率的大小来达到分类目的。线性回归的预测结果为整个实数域,因此为了将分类器输出界定在 $[0, 1]$ 之间,引出了 sigmoid 函数。并通过将对数极大似然的变换定义为损失函数,对 sigmoid 函数中的参数使用梯度下降进行估计。最后对比分析了线性回归和逻辑回归的区别,线性回归是在拟合输入向量 $X$ 的分布,而逻辑回归中的线性函数是在拟合决策边界。
感谢参考资料的各位作者的精辟分析,本文中部分内容直接拿来主义,再次感谢。

