继续！

费马(Fermat)引理

设函数 $f(x)$ 在点 $x_0$ 的某领域 $U(x_0)$ 内有定义，并且在 $x_0$ 处可导，如果对于任意的 $x \in U(x_0)$，有

$$f(x) \leq f(x_0) （或 f(x) \geq f(x_0)）,$$

那么 $f^{‘}(x)=0.$

罗尔(Rolle)定理

如果函数 $f(x)$ 满足

• 在闭区间 $[a, b]$ 上连续；
• 在开区间 $(a, b)$ 内可导；
• 在区间端点处的函数值相等，即 $f(a)=f(b)$，

那么在 $(a, b)$ 至少有一点 $\xi，(a<\xi<b)$，使得 $f^{‘}(\xi)=0.$

拉格朗日(Lagrange)中值定理

罗尔定理中 $f(a)=f(b)$ 是相当特殊的，使得罗尔定理的应用受到限制，如果取消 $f(a)=f(b)$ 这个条件，但仍然保留另外2个条件，并相应的改变结论，就得到 拉格朗日中值定理。

如果函数 $f(x)$ 满足

• 在闭区间 $[a, b]$ 上连续；
• 在开区间 $(a, b)$ 内可导；

那么在 $(a, b)$ 内至少有一点 $\xi，(a<\xi<b)$，使得等式

$$f(b)-f(a)=f^{‘}(b-a)$$

成立。

改写上式可以表达为

$$\frac{f(b)-f(a)}{b-a}=f^{‘}(\xi)$$

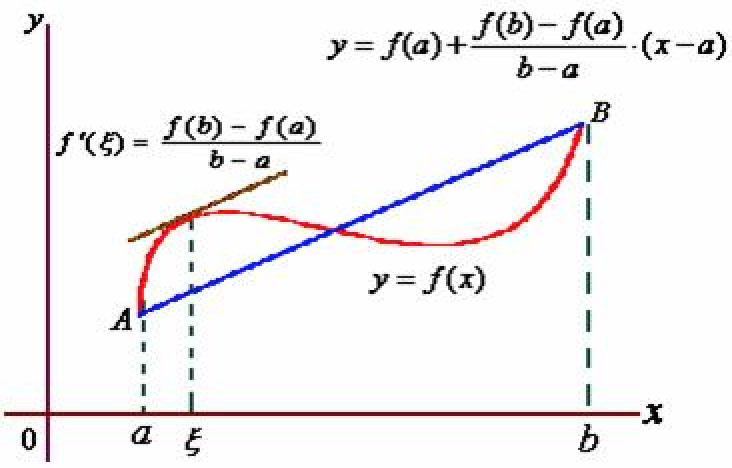
拉格朗日中值定理的几何意义为：如果连续曲线 $y=f(x)$ 的弧 $AB$ 上除端点外处处具有不垂直于 $x$ 轴的切线，那么这弧上至少有一点 $C$，使曲线在点 $C$ 处的切线平行于弦 $AB$。

柯西中值定理

如果函数 $f(x)$ 及 $F(x)$ 满足

• 在闭区间 $[a, b]$ 上连续；
• 在开区间 $(a, b)$ 内可导；
• 对任一 $x \in (a, b)，F^{‘}(x) \neq 0$，

那么在 $(a, b)$ 内至少有一点 $\xi$，使得等式

$$\frac{f(b)-f(a)}{F(b)-F(a)}=\frac{f^{‘}(\xi)}{F^{‘}(\xi)}$$

成立。

很明显，如果 $F(x)=x$，那么$F(b)-F(a)=b-a, F^{‘}(x)=1$，因而上面公式可写为

$$f(b)-f(a)=f^{‘}(\xi)(b-a), (a<\xi<b),$$

这就变成拉格朗日中值公式了。

洛必达法则

如果当 $x \to a（或 x \to \infty）$时，两个函数 $f(x)$ 与 $F(x)$ 都趋于零或者无穷大，那么极限 $\lim \limits_{x \to a} \frac{f(x)}{F(x)}（或 \lim \limits_{x \to \infty} \frac{f(x)}{F(x)}）$ 可能存在、也可能不存在，例如 $\lim \limits_{x \to 0} \frac{sin(x)}{x}$。

洛必达法则 $L^{‘}Hospital$ 就是解决这类问题的，这种在一定条件下通过分子分母分别求导再求极限来确定未定式的值的方法称为洛必达法则。

当 $x \to a$时，未定式 $\frac{0}{0}$ 的情形，设

• 当 $x \to a$ 时，函数 $f(x)$ 及 $F(x)$ 都趋于零；
• 在点 $a$ 的某去心领域内，$f^{‘}(x)$ 及 $F^{‘}(x)$ 都存在且 $F^{‘}(x) \neq 0；$
• $\lim \limits_{x \to a} \frac{f^{‘}(x)}{F^{‘}(x)}$ 存在（或为无穷大），则

$$\lim \limits_{x \to a} \frac{f(x)}{F(x)}=\lim \limits_{x \to a} \frac{f^{‘}(x)}{F^{‘}(x)}.$$

当 $x \to \infty$时，未定式 $\frac{0}{0}$ 的情形，设

• 当 $x \to \infty$ 时，函数 $f(x)$ 及 $F(x)$ 都趋于零；
• 当 $|x| > N$ 时 $f^{‘}(x)$ 及 $F^{‘}(x)$ 都存在且 $F^{‘}(x) \neq 0；$
• $\lim \limits_{x \to \infty} \frac{f^{‘}(x)}{F^{‘}(x)}$ 存在（或为无穷大），则

$$\lim \limits_{x \to \infty} \frac{f(x)}{F(x)}=\lim \limits_{x \to \infty} \frac{f^{‘}(x)}{F^{‘}(x)}.$$

文中图片来自 维基百科。

参考资料

1. 《高等数学》，第七版上册，同济大学版